Most people agree that support of people, who cannot support themselves is a good idea. People just tend to disagree on the degree to which this should happen. In this post, I’ll argue that having high taxes makes everybody lose out (the society and all workers) whereas lower taxes will make everybody richer.
High Taxes and the Nash Equilibrium
Assume we are in a high-tax country taxing income at 70%.
Since one of the countries, I know the best is also the country in the world with the highest taxes, let’s use Denmark as example (link is to an old document, but aside from the amounts, it is still mostly correct). In Denmark you pay 8% of your gross salary in AMBI (ArbejdesMarkedsBIdrag – basically a tax on actually working). After that you pay for health insurance (8%), for your local government (typically around 25%), for your nation government (5.5%), if you earn more than DKK 350.000 (mellemskat or middle tax at 6%) or if you earn more than DKK 350.000 (topskat or top tax at 15%; the limit for mellemskat has recently been increased to the same level at topskat, it used to lower). In total that is 8% tax followed by 8% + 25% + 5.5% + 6% + 15% = 59.5%, which is generously capped at 59%, so for each 100 CU (currency unit) you earn, you get 100 * 0.92 = 92 after AMBI and 92 * 0.41 = 37.72. So, after tax you get paid 37.72 CU for each 100 CU you earn. The taxation does not stop there, though, as the VAT in Denmark is at 25% of the price of goods, meaning that 20% of the price you pay in stores is really just tax, you only get spending power corresponding to 37.72 * 0.8 = 30.176. That is only if you are not stupid enough to purchase anything on which there is additional taxation (like anything with sugar in it, anything using energy to produce or, Britney forbid it, anything with alcohol in it or something in general that could be bad for you). In total, the 70% taxation is not that far-fetched. As most people who are actually working full time reach the top-taxation, I find it reasonable to use the taxation including top-tax, as this is the taxation you chop off first by working less.
Assume now we have two persons, A and B. A earns 1500 CU for a day’s work (before tax) any B earns 1000 CU a day (also before tax). Now A wants to purchase a service from B. It could be building a shed or something like that. The work will take B a day of work, but A can do it himself in 2 days work. Now, in order for A to pay B 1000 CU to do the work, he has to earn 1000 / 0.3 = 3333 or roughly 2 and a quarter day’s work. As A can do the work himself in just 2 days, he’s better off taking two days off work (sans salary) doing the work himself and cashing in (3333 – 2 * 1500) * 0.3 = 100 CU (after tax himself). Naturally B will miss out on a day’s salary. In order to get the job, he’d have to lower his price to 2 * 1500 * 0.3 = 900.
In the first case, the state earns by taxation exactly 0, as A does not make any money by taking 2 days off and B is unemployed – it may in fact be down support to B corresponding to a day’s pay, i.e., 1000 – 1000 * 0.7 = 300 (the salary minus taxation of the support). A also earns 0, but this is still better than the -100 CU he’d have by having B perform the task. B earns 0 or 300 (depending on whether we live in a social state or not). If B prices a day’s work instead at 900, the state earns 2 * 1500 * 0.7 + 900 * 0.7 = 2730, A earns 0 (same as before) and B earns 900 * 0.3 = 270.
Assuming we do not live in a social state, B increases his pay by 270 CU by lowering the price, but if we do live in a social state, he instead lowers his pay by 30 CU. Of course, he’s not gonna do that, so the state is down 300 CU (instead of being up 2730 CU) and B is up 30 CU. For A it does not matter either way.
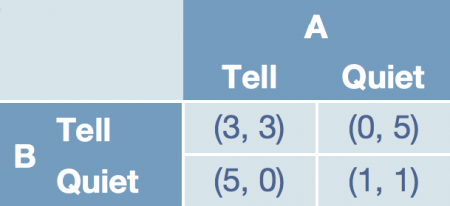Now, the idea of the Nash equilibrium is that by altering one’s own behavior from maximizing for yourself regardless of the strategy of others, you can get a solution that is better to everyone. Compare this to a soccer match. If both teams play against each other, they have to run around like idiots for 2 * 45 minutes, eventually possibly having one team or the other score more goals. If they don’t the other team will score heaps of goals, and the team loses. If they just agree that soccer sucks (it’s almost part of the name anyway), and go out for a couple cold ones, they both get a draw, but have instead a nice time for an hour and a half. The classical example is that of two criminals. The police does not have enough evidence to commit them for a long time, but if one of the rats out the other, they can. They therefore propose to both that if they rat out the other, they get off free if the other keeps silent, causing the other criminal to get 5 years of prison. If both cooperate, both get 3 years of prison and if both keep silent, they both get 1 year of prison. If you do not know what the opponent do, you rat him out. The reason is that assuming that the probability for each outcome of the opponent is 50-50, your expected prison time is 3 * 0.5 + 0 * 0.5 = 1.5 years of prison, whereas if you keep quiet, your expected prison time is 1 * 0.5 + 5 * 0.5 = 3 years. By agreeing with your partner to both keep quiet (and assuming that criminals can be trusted), instead your expected prison time is 1 * 1.0 + 5 * 0.0 = 1 year. As this is symmetric, the same holds for the other criminal, and so both win on agreeing on what is otherwise the sub-optimal choice for each.
The same holds for taxation. Assume we live in a social state. Naturally, B will keeps his prices at 1000 CU, earning 300 CU from the state. A will take a couple days off and do the work himself, earning 100 CU (from -100 CU to 0 CU), and the state will be out 300 CU for the support payment to B. If instead the tax was decreased to 65%, A would suddenly only have to earn 2857 CU to pay B 1000 CU, which is less than the amount he could earn in the two days, he’d have to work to do the work himself, so instead he pays B to to the work. Now the calculation is: state: 2 * 1500 * 0.65 + 1000 * 0.65 = 2600, A: 2 * 1500 * 0.35 – 1000 = 50, B: 1000 * 0.65 = 350. This shows that all of the state, A, and B are better off! The state is up 2600 CU instead of being down 300 CU, A is up 50 CU instead of being at 0 CU, and B is up 350 CU instead of 300 CU.
By decreasing the ration of time A needs to perform B’s job, we can repeat this calculation for any amount of taxation (in the above example, the sweet spot for the state is to put taxation at x, where 1000 = 2 * 1500 * (1 – x) implying that x = 1 – 1000 / 2 / 1500 = 1 – 1/3 = 66.7%). By making the ration (2 in the example) go towards 1000 / 1500 = 2/3, we make x go towards 0 (for example if A needs to use the same amount of time as B to perform the task, only a taxation below x = 1 – 1000 / 1 / 1500 = 33.3% would make him do it). If the time A has to use to do a job instead of B drops below 2/3, it will never be better for him to make B do it.
Just to overcome one possible complaint: in the above calculation, somehow 2 * 1500 (A’s salary) appeared to be added to the system. In a closed system, this should not be possible, right? Wrong. The 2 * 1500 CU comes from the extra production caused by making A do his job instead of having him waste two days of doing B’s job (while B is taking a day off).
The Social State, the Salami Method, and the Dictatorship of Democracy
By the above calculations, we can argue that no taxation is best for everybody, but even then, most agree that some common obligations are worth undertaking. Such may include welfare, healthcare, infrastructure and public transportation, or painting all trees blue. Each of these would have some value to people, but the value may differ from person to person.
Suppose we have a society of three persons, A, B, and C. A and B each 1000 CU a day, but C is unemployed. B and C are related. Now, the society decides that welfare is the new pink, and has to vote at which level it should be. A is not really interested (he can see who is going to be the losing part), C is very interested (he only stands to gain money from this), and B is slanted towards yes (as he otherwise has to support his “artist” relative). Now, both B and C votes for welfare, while A votes against. After that, they have to decide on the amount. A has a low probability of getting anything out of this, and so welfare is only worth, say, 10 CU (1% taxation) for him. For B it’s worth, say 300 CU or 30% (the amount he pays to support paint and drugs to his relative), and for C it’s worth all he has got (which is nothing), i.e., 100%. If they vote, they can arrive at a taxation of 30% (the median) or 43.7% (the average). Now, to make ends meet, A and B are taxed to support C. C in turn pays the same amount of tax of his support, so he does not get the full 30% or 43.7% of the other’s salaries, so after taxation and welfare, A and B earn 1000 * 0.7 = 700 or 1000 * 0.563 = 563 CU, and C gets 2 * 300 * 0.7 = 420 or 2 * 437 * 0.563 = 492. After this, the state has money left, which can be distributed according to the amount of taxed you have paid, yielding (2 * 300 * 0.3) * 300 / (2 * 300 + 0.3 * 2 * 300) = 69 or (2 * 437 * 0.437) * 437 / (2 * 437 + 0.437 * 2 * 437) = 133 to A/B and (2 * 300 * 0.3) * (0.3 * 2 * 300)/ (2 * 300 + 0.3 * 2 * 300) = 42 or (2 * 437 * 0.437) * (0.437 * 2 * 437) / (2 * 437 + 0.437 * 2 * 437) = 116 to C, yielding a total of 720 + 69 = 899 or 563 + 133 = 696 to A and B and 420 + 42 = 464 or 492 + 116 = 608 to C.
As we see, in this dystopia, which is built on democracy, in the case where the agreed-upon tax is 30%, B and C have managed to vote themselves to part of A’s money. This trend of course only gets worse as the fraction of people leeching off of others increases. In the case where the agreed taxation is 43.7%, C manages to cheat both A and B (though A could decrease the value of welfare to 0 CU, voting 0%, and B could decrease the value to 200 CU, voting 20%, making B in the end get 714 CU, which is still better than the 700 CU he’d have by supporting his leeching family member). The money B pays to C can also be eliminated, making B instead calculate a probability of becoming dependent of welfare himself. As long as the number of people producing value is higher than the number of consuming, the optimal, yet somewhat unsympathetic solution is for 0 taxation and just letting the rest die. Naturally, people are able to assign a value a service even if they do not immediately gain from it themselves. In the society C was the only one who really gained from welfare, but B saw a purpose in supporting this, so he got welfare.
Applying the salami method, i.e., making you swallow something you could not initially by cutting it up in smaller pieces, A and B may agree on a hospital service, A and C may agree on public transportation, and so on. In this way, you collectively decide on adding more expenses, where each expense has a majority, but the combined expenses may not. If, for example, everybody were willing to pay 400 CU in taxes, and welfare, healthcare and public transport each costs 200 CU, the aforementioned scenario makes sense: each only votes for expenses accumulating to 400 CU, but the combined expenses, imposed on everybody, are 600 CU.
This principle can even be exploited even further. In the society from before, B gets a car, and wants roads. A does not have a car and is already dissatisfied with the taxes and is for public transport, so he is against. C is unemployed and does not want to use his (lower than A’s or B’s) salary on that. Instead C really likes blue trees. He therefore strikes a deal with B: if you support painting all trees blue, I support building roads. Now both have majority for their proposal, even though none of the proposals had majority. As an added bonus, they even get to make A pay one third of the expenses for cars and painting all trees blue. This is the dictatorship of democracy: even though you are a majority, you may impose your ideas on others as long as you can find somebody with an even more ridiculous plan to support you in exchange for support of their idea.
