CPN Tools 4 adds a couple new types to make modeling easier. The new types are intinf, real and time. These types makes it easier to construct readable models as we no longer have to represent large numbers using strings, we can use real values without any rounding, and we can directly embed time stamps in tokens without any configuration.
Large Integers (intinf)
The intinf type works exactly like regular integers, except they do not have an upper bound. A new standard declaration for intinf types is created for new models as INTINF.
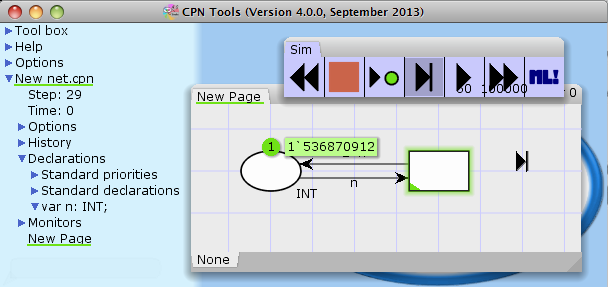
Regular integers have bounds. For technical integers are 31 bit signed values, meaning they can take values -1,073,741,824 = -230 – 230-1 = 1,073,741,823. If they get larger, the CPN simulator simply overflows and often yields an erroneous result. For example, consider the below model always doubling the value of the token:
The value of the token is currently 229 = 536,870,912. Doubling the value, leads to the value 230 = 1,073,741,824 > 1,073,741,823 and hence an overflow. This is not handled very nicely (the tool assumes you don’t overflow values), and this is the result:
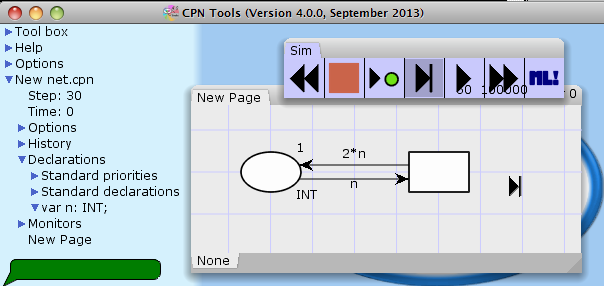
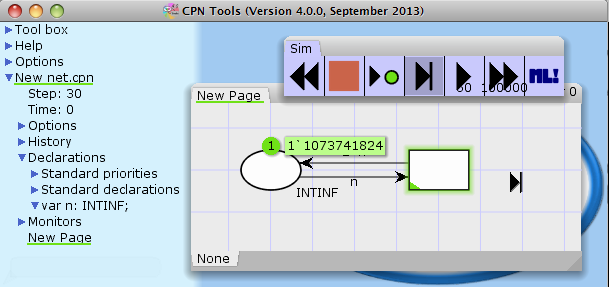
Simply switching from INT to INTINF (for the place and the type of the variable n) removes this problem:
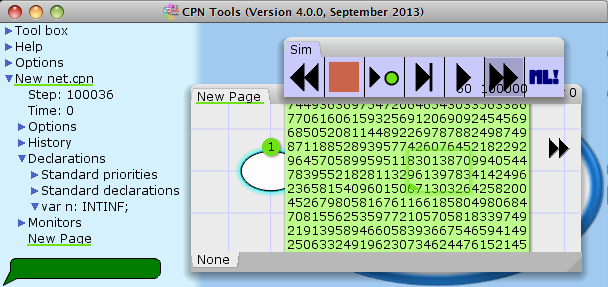
The problem is not just postponed, but really removed:
(The token has a value with amore than 30,000 digits in base 10.)
The only reason for not completely replacing regular integers with large integers is that computation is marginally slower (this does not matter in practice) and they do take up significantly more memory, so especially for state-space analysis using regular integers is often better (if you need the full power of large integers, state-space analysis is not applicable anyway).
Real Values (real)
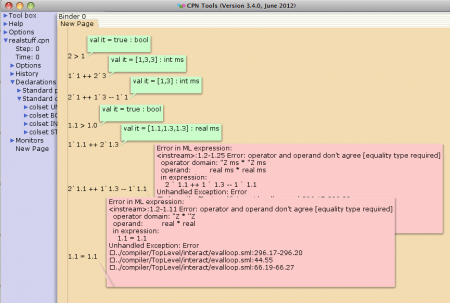
It seems supporting real values is a trivial feat. Just do the same as needed to support large integers or any of the other types. For some operations, that is also true, but not for all. To illustrate the problem, consider the below:
We see three operations on integers: comparison, multiset addition, and multiset subtraction. They naturally yield the expected results. We then try the same three operations on real values. Comparison is good as is multiset addition. For multiset subtraction, we get an error which boils down to something with “equality type.” Digging deeper, we see that we cannot even test equality between two real numbers.
This is a feature of Standard ML and it makes sense. It basically boils down to floating point values not adhering to the assumptions for equality types in Standard ML, which means there is a lot of things we can do on integers/strings/records/… we cannot do with reals. We can do basic simulation, as it only relies on inequality, but anything but the simplest models fail, and using reals in functions leads to strange behavior in many cases. Also, the state-space tool relies on types being equality types, so using real means no state-space analysis.
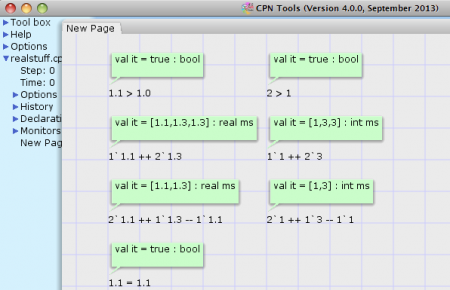
For CPN Tools 4, we changed the compiler so that it allows real to be an equality type. This means that all the above expressions evaluate nicely in CPN Tools 4:
This means, we can now create models like this:
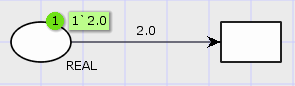
While possible, we recommend against using equality comparisons for reals as rounding errors lead to numerical instability and uexpected results like here:
While the value is displayed as 2.0, it is really entered as 2.000000000000001. As this is not the same as 2.0, the transition is not enabled. This can happen due to rounding errors in computations as well, so it is better not to make models rely on equality of reals.
It is in fact better to not let your model rely on the values of reals at all. They can be useful for making measurements with non-integer values, which is perfectly fine. If needed, you can use inequalities (for example to filter “widgets” which takes more than 5.0 time units to process), but be aware that there may be rounding errors.
Aside from rounding errors, real types work exactly like any other type starting with CPN Tools 4.
Time Values (time)
CPN Tools supports two kinds of time stamps: integers (really large integers) and reals. With the support for large integer and real types, it is now possible to store time stamps directly in tokens instead of resorting to translations to strings. This is good for legibility and accuracy.
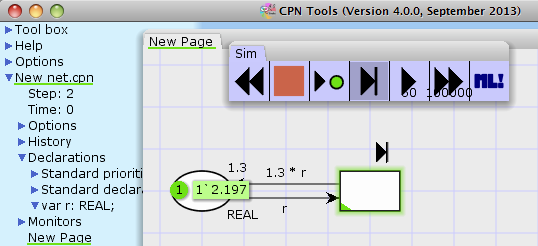
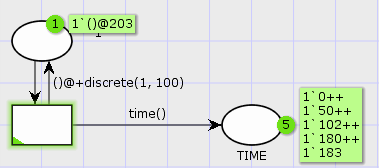
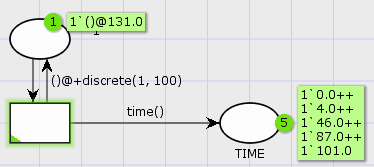
Instead of relying on the implementation of time stamps, it is possible to create a variable of the type time (TIME in the standard declarations). This automatically fits the current kind of time stamp. This is good for those rare cases where the type of time stamp is changed, but also for documentation. The type works exactly as either large integers or reals.
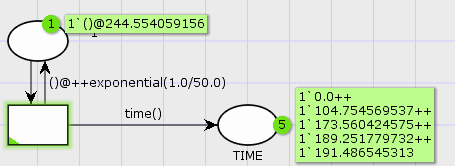
We see that the exact same model works both with integer time and real time. Naturally, we’d probably use a distribution that actually produce non-integer values, like this:
Too see a live demonstration of these colorsets and their use, check out this video:

Please I need help on how to write lognormal and triangular distribution functions in CPN tools
I am interested in Knowing more about information on CPN.
I would recommend either of the books listed at http://cpntools.org/2018/01/16/publications/; Kurt’s book is more theoretical about the language, while Wil’s book is more about application, especially within business process modeling.