 I just finished the implementation of colored automata in Declare. The formal foundation is described in
I just finished the implementation of colored automata in Declare. The formal foundation is described in
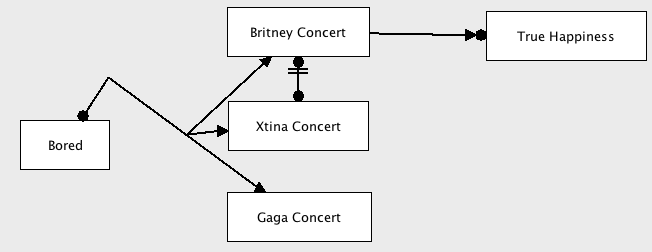
The idea is that normally we construct an automaton accepting only all valid executions. Assume we look at the model:
The model says that “if you are bored, you should go to a concert” (the reponse constraint from Bored to the the Concerts), “you can never go to both a Britney and a Xtina concert” (the non-coexistence constraint between Britney and Xtina Concerts), and “only after going to a Britney Concert, can you be truly happy” (the precedence constraint from Britney Concert to True Happiness).
Normally, we would translate it to this automaton:
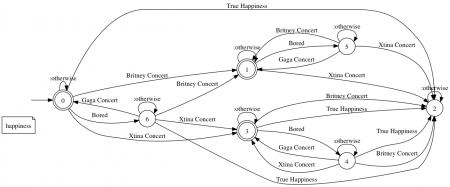
Click for a larger version. States with a double outline are states where all constraints are satisfied and states (there’s only one) with a dashed outline are states where at least one constraint can never be satisfied. To just enact the system, this is fine. Sometimes we wish to provide more information, such as indicating that some constraints are not currently satisfied. For this we annotate each state with the state of the individual constraints and obtain this automaton:
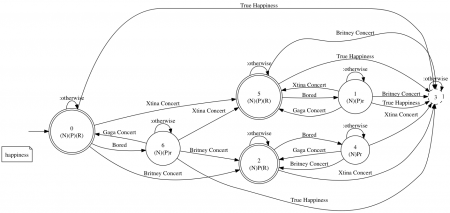
We use the first letter of the constraints (N = non-coexiststence between Britney and Xtina, P = precedence that happiness can only occur after a Britney concert, and R = response that after being bored we have to go to a concert). A letter in upper-case means that the constraint is satisfied in the state. If the letter is in parentheses it means that it is possible to execute tasks that makes the constraint violated again. A letter in lower-case means that the constraint is currently not satisfied but it is possible to execute tasks to make it satisfied.
This automaton is excellent for enactment in a controlled environment as we have information about all constraints available in constant time. If we cannot control the actions of the user, we can only provide diagnostics. For this, we need to be able to continue after an error. For this, we make the full automaton:
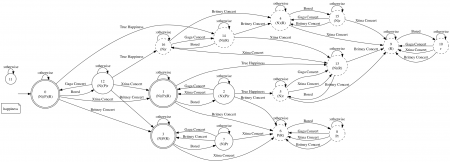
This automaton furthermore has states with fewer than 3 letters; letters that are absent are constraints that are never possible to satisfy again. In the figure, most of these states are at the top. We basically expand the state 3 from the previous figure to provide diagnostics as we continue execution. In the above example, we see that if we execute “True Happiness” without first going to a Britney concert, we no longer can satisfy the precedence constraint. If we continue the execution, we work our way towards a part where it is also no longer possible to satisfy the non-coexistence constraint, because we have been to both a Britney and a Xtina concert. We also see that it is always possible to satisfy the response constraint (simply by going to a concert).
These automata are exported directly from the Declare Designer:
Declare currently doesn’t use the colored automaton internally. This feature is available now from the Subversion repository and will be part for Declare 2.4.


One thought on “Colored Automata in Declare”