The past weeks, I’ve been working on what was intended to be a small amusing feature in the Model-Based Testing Workbench, but instead turned out to be much more complex and useful than I thought it would be.
Fuzzing is a testing technique, which consists largely of just throwing random inputs at a program and observing how it reacts. Half a decade ago, I attended a talk by a guy from Microsoft, who claimed that (a new approach to) fuzzing was the largest contributor to Microsoft solving their security issues. Remember?Until 10 or so years ago, you would get monthly reports about another handful of severe leaks in Windows during patch Tuesday. Then it just sort-of stopped, and all attention turned to Adobe instead. What I am saying is that fuzzing is a very, very good technique which in addition is fully automatic and can applied with very low cost.
Regular fuzzing (black-box fuzzing) just consists of sending random input to programs and can therefore be fully automated. This means it is very cheap to implement, but also that the gains si relatively low. Due to the randomness of the tests, they will test a lot of fair-weather scenarios that are handled correctly, and only with low probability will touch risky edge cases.
As an alternative, white-box fuzzing was developed. It is based on morfe or less heavy-duty analysis of the program under test. The goal of the analysis is to come up with inputs that try to touch as much of the code as possible. The disadvantage of this method is the usage of formal methods, which require quire a lot of investment to get running, but the promise is that it will find more bugs and might even assist in proving absence of bugs using model-checking techniques.
Microsoft pioneered a combination, dubbed gray-box testing, which doesn’t rely on heavy-weight techniques like model-checking, but instead uses random inputs, and relies on code instrumentation to mutate this input to touch as many parts of the code as possible.
I wanted to integrate fuzzing techniques into the MBT Workbench. The MBT Workbench is an implementation of tool support for model-based testing. The idea of the MBT Workbench is that we have input and output mappings which translate between the model domain and the real-world domain. An input mapping translates input parameters to a model into requests to a web-service, and an output mapping translates responses from a web-service into output variables that match those of a model. Testing then comprises comparing the value you get by running all combinations of input parameters thru the model and thru the input mapping, web-service, and output mapping. The tool assists the user in constructing all artifacts necessary for testing.
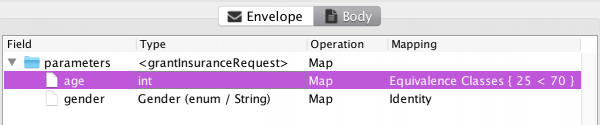
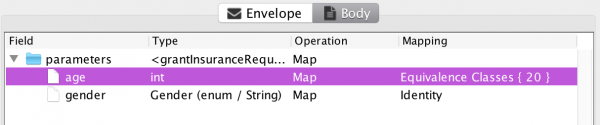
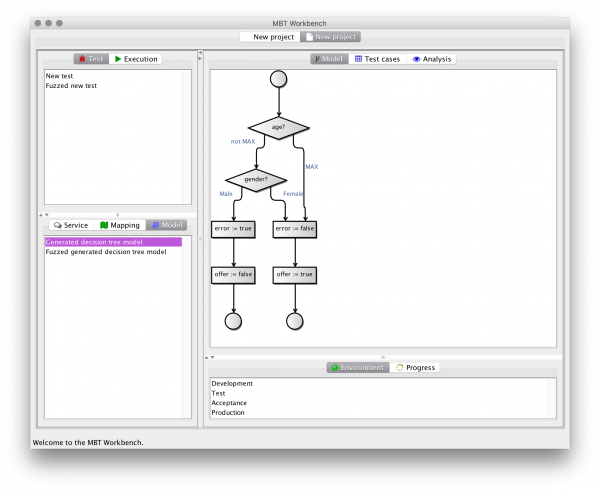
The artifact that currently requires the most user-interaction is the input mapping. The MBT Workbench can generate all other artifacts more or less automatically, but it needs the user’s input to provide a good starting point for the analysis. For example, an insurance company granting car insurances but not to young men under the age of 25 (due to risk), could provide a web-service for this. In the MBT Workbench, setting up the input mapping could look like this:
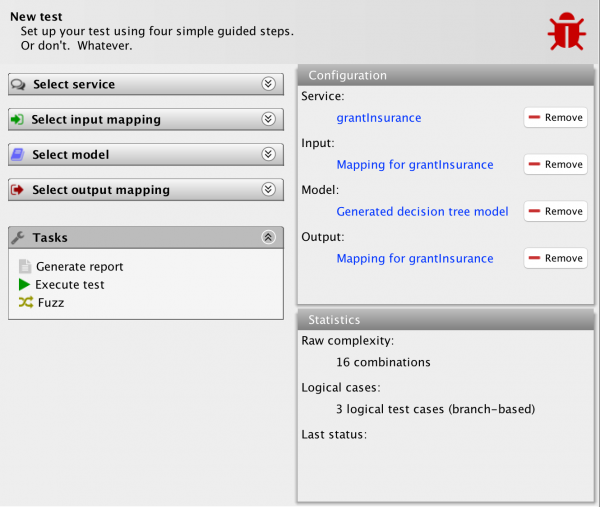
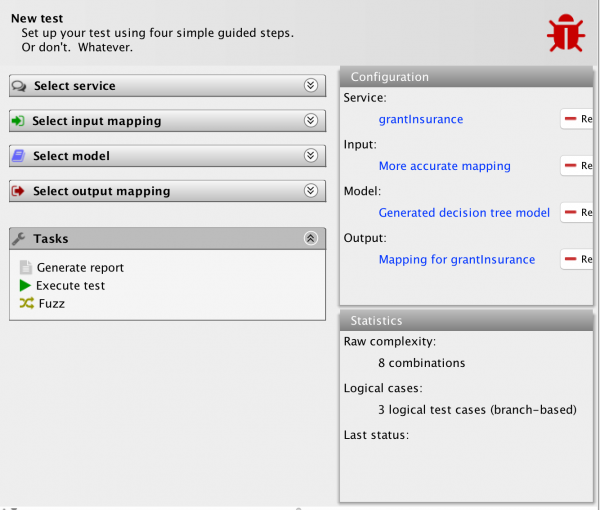
We have specified that all possible genders should be tested using an identity mapping and that we should test the age using automatically generated equivalence classes based around 25 and 70 being important values. Everything is generated automatically, except for the input of those two magical values. Why 25 and 70? 25 is the only number mentioned in the specification and 70 came from a pedagogical point I made half a dozen posts or so. But how do we know these values are the ones that matter? Enter fuzzing! Assume, I have set up a full test based on the above input mapping:
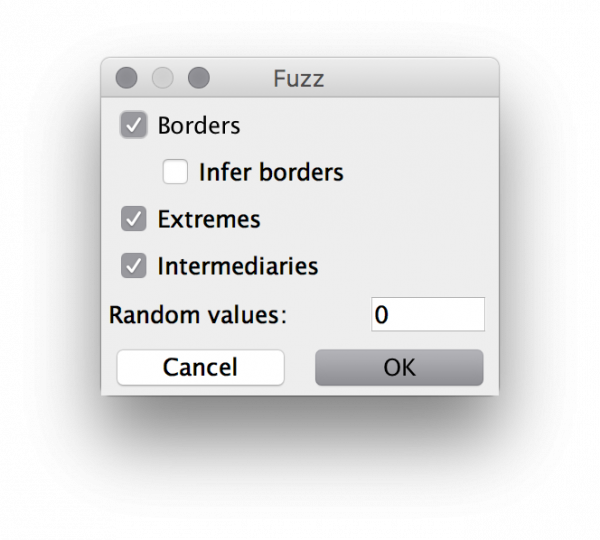
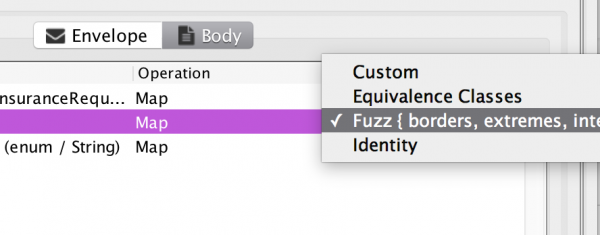
We see we now have another action available, to fuzz the test. If I select that action, I am greeted with this screen:
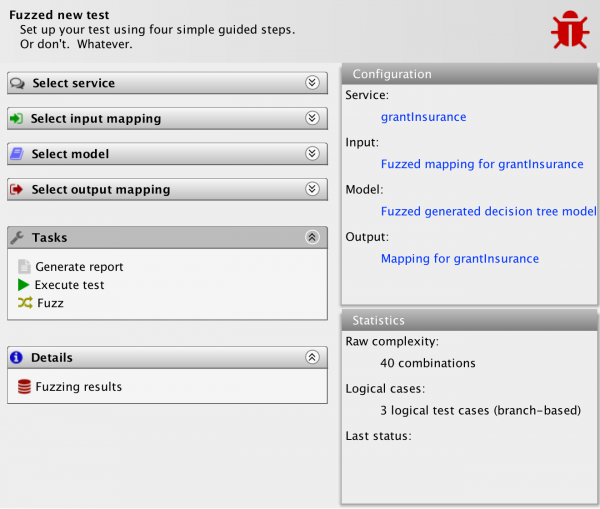
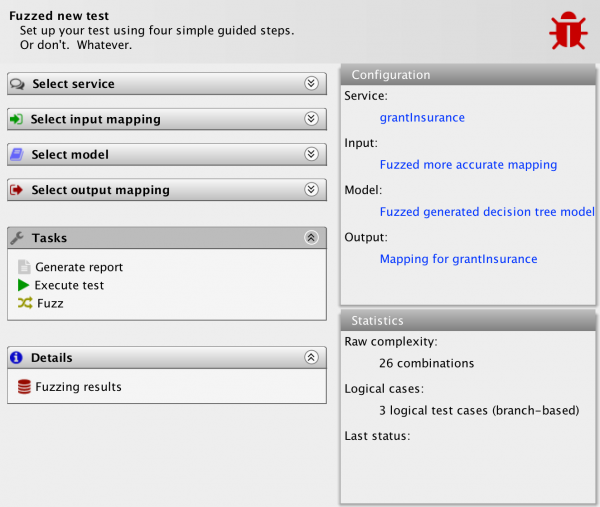
The tool is asking me to set up an updated input mapping based on the existing one. I provides a new mapping type, the Fuzz mapping, which is selected automatically for appropriate inputs. Everything in the above view is created automatically, and only provided to allow me to perform any customizations I would like to. Just pressing accept, just displays another test screen:
The tool has generated a new input mapping based on my above selections and a new model as well. We notice that the raw complexity of the test has gone up from 16 combinations to 40 combinations, but the logical complexity remains at the 3 logical test cases. I also have a new action available, to review the fuzzing results. Let’s do that:
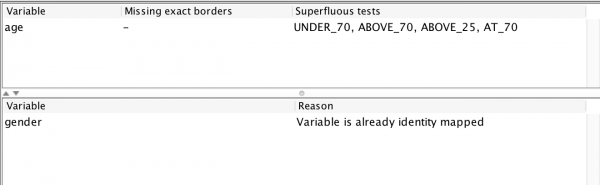
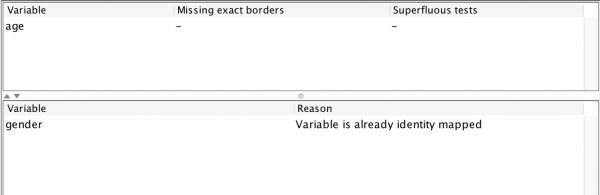
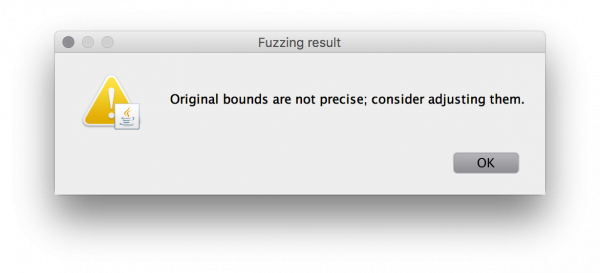
The view displays feedback on my test configuration. Starting from the bottom, it mentions that the gender variable has not been tested because it is already exhaustively tested. The report also informs that the age variable is performing 4 superfluous tests (all the tests around 70 and the one testing a value “above 25.” It also informs me that I am missing no borders as far as the fuzzing is aware. Let’s use this (100% automatically obtained!) information to set up a new input mapping:
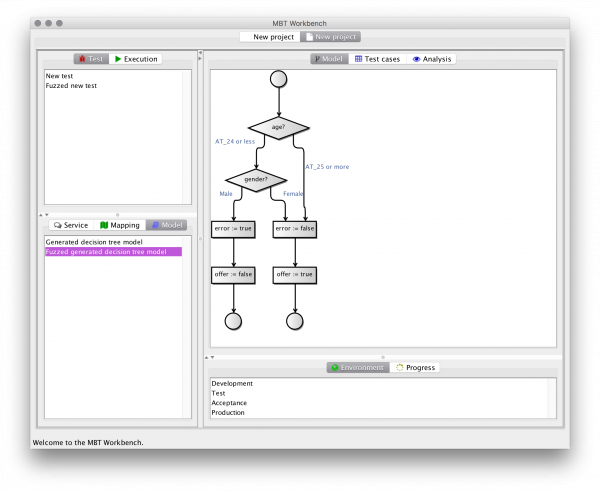
We use the new syntax to allow me to precisely describe the border to test as 24/25 (instead of just specifying that everything around 25 should be tested), and removed the superfluous value 70. You get one guess as to why that new syntax was introduced. Our updated test:
We have halved the raw test complexity. Let’s fuzz:
…and check the results:
We get no comments. We should still run the fuzzed tests to confirm the results, but we now see that the test is minimal and complete, i.e., as far as the tool is aware, we are now testing all relevant values and out test suite contains no superfluous tests.
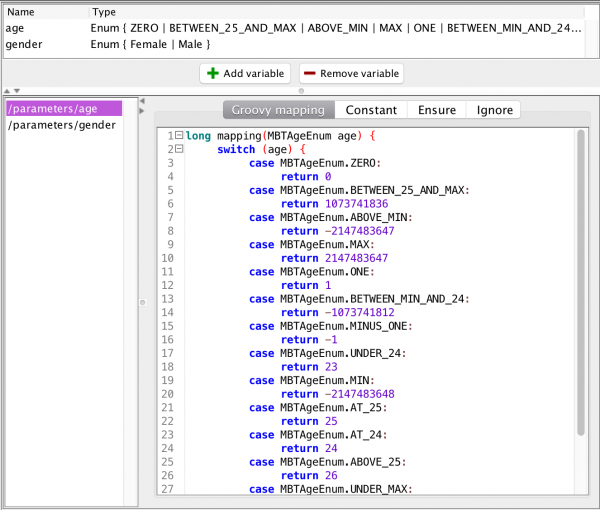
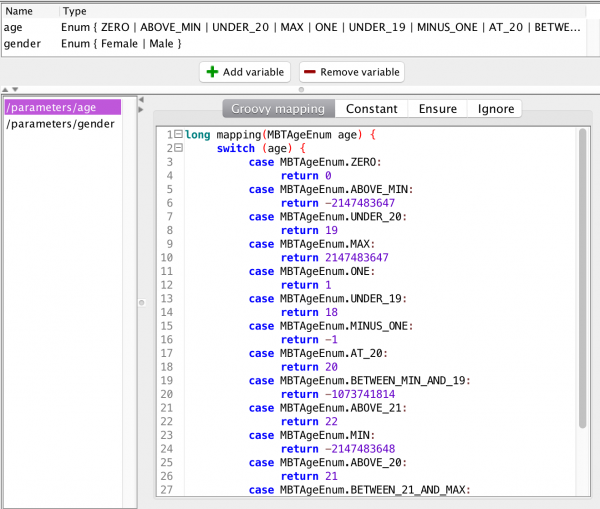
How did it do this? Well, it added some more values to the input variable. If we inspect the generated fuzzed more accurate mapping, we see it maps a lot more values:
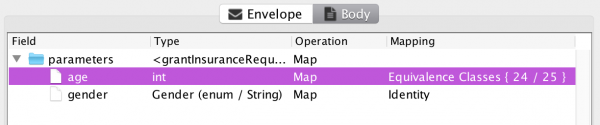
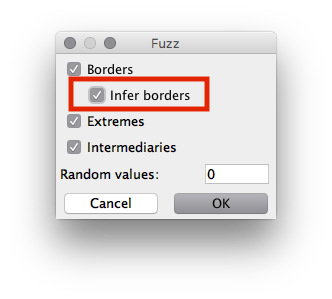
What precisely happens, is probably easier seen if we look further into the configuration of the mapping:
The new mapping is testing all borders of existing values, hence why it is adding the UNDER_24 and ABOVE_25 values (and ABOVE_MIN and UNDER_MAX). We have also instructed it to test extreme values. Here, it’s adding the MIN and MAX values (if they don’t already exist – in this case they do) as well as ZERO, ONE, and MINUS_ONE values to test often-encountered special values. Finally, in this configuration, it is adding values in-between all existing values. It can also be configured to add any amount of random values to test.
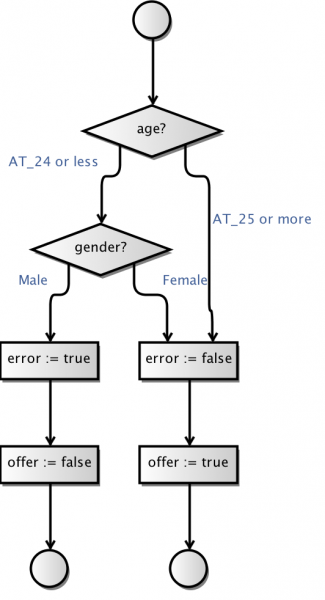
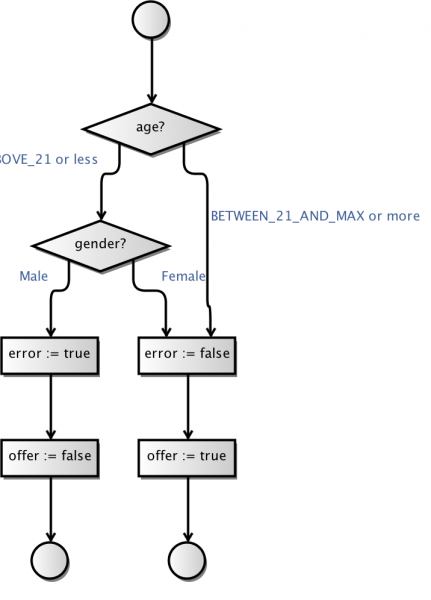
After generating the new model, it needs to extend the model to also handle the new input values. Luckily, I just extended the MBT Workbench models so they can have more elaborate choices comprising sets of values. There is no visual difference between the original model and the fuzzed model, but now the “or less”/”or more” catch-all refers to many more logical test values:
The fuzzed model often much larger than the original model and therefore not suited for nor intended for regular testing. It should just be run once to ensure that the overall operation is still correct. The fuzzer makes some invocations during the process to correctly categorize some values in some cases, but does not perform a comprehensive test (the test module is better for this anyway). Testing the fuzzed model (after taking relevant suggestions into account) is intended to ensure that the original test is sensible.
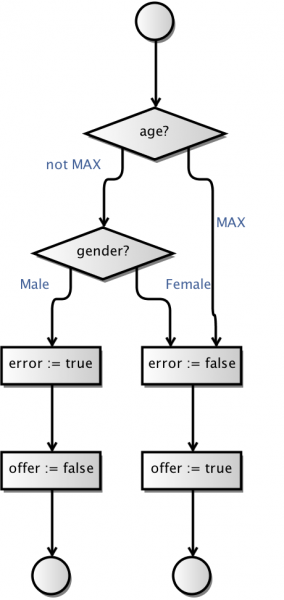
So, this was a simple fair-weather execution of the fuzzer. What if it finds issues with the original test? Well, assume that I has mis-read the specification, and thought the age-limit instead was 20 years?
This results in a rather weird model:
But all tests are green, and perhaps this is part of a larger test effort, so we don’t notice. The fuzzer does:
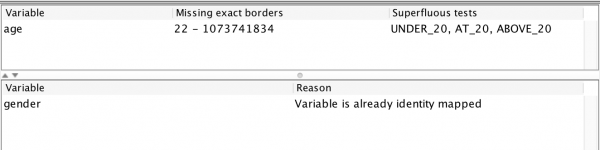
The fuzzing report clearly explains what the issue is:
The age mapping contains superfluous tests around 20. In other words: the border we input means nothing. It also detects that that the appropriate border is in the interval 22-1,073,741,834, and an updated model reflects this “improvement:”
Of course, an interval of more than one billion is not very helpful, but luckily the fuzzing options can help us narrow that down to an exact value.
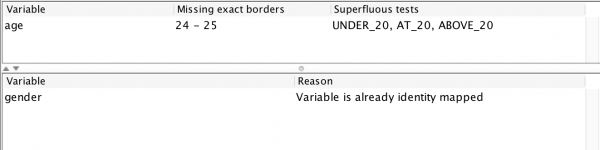
The fuzzing operation has helped us find the correct border of 24/25, and derived a much better model:
We see that the tool has assisted us in vastly improving our test. Luckily, the new mapping method tries to encompass the entire behavior and catches and fixes the issue in a single step. The old mapping method would only have revealed the issue during running the fuzzed test and would have needed another improvement step to also fix the issue.
I call the operation pink-box fuzzing. It’s my method so I god-darn-it get to name it. Also, it’s not quite gray-box fuzzing, nor is it really white-box fuzzing, and I thought that 50-shades-of-gray-box fuzzing sounded retarded.
The tool tries to find a consistent extension of the model under the assumption that the original test is complete. This means that if a fuzzed value is between two values that are sorted the same in a decision node, it too is sorted the same. This relies on the new concept that variables comprise ordered values. In this way, for example, ZERO will be put in the branch that checks the gender because both MIN and UNDER_20 are sorted in the same branch.
Values that fall between two values on either side of the choice are sorted into groups using a simple binary search algorithm, which tries to find the value that should rightfully be in the test. It tries to match each value with other values on the one side of the branch and if successful applies the “all values between two values on the same branch rule” to categorize half of the remaining values.
Superfluous values are values that are never essential to any choice. In our first example, the values with 70 were not-essential, because the only choice is about what happens at age 25. If the model were larger and contained more choices, 70 might be important, but in this example it is not.
Missing borders are borders where the largest value on one side of the choice is more than one smaller than the smallest value on the other. The tool can search these using regular numerical binary search using a similar categorization approach as is applied during the categorization on in-between values.
This function does not guarantee it will find all borders, but if it is given a value on each side of a border, it will find an appropriate border. If there’s more borders the approach may or many not find it. If the user inputs something just resembling reasonable, it is very likely that this procedure will improve or entirely fix the test.